Úvod
O této metodě, která se dá použít například i v kasinu, se můžete dočíst i ve starším článku na tomto portálu: Obchodování na bázi Martingale. Autor článku se soustředil na praktické aspekty Martingale obchodování a uvádí i konkrétní výsledky ze simulace v platformě MetaTrader. My se naopak zaměříme na teoretické vyhodnocení pravděpodobností zisků a ztrát a provedeme i některé potvrzující simulace.
Autor ve zmíněném článku uvádí, že "...obchodování na základě Martingale ruletního systému je možný, že systém má určitý potenciál, i když s sebou nese určité riziko jako většina systémů a že do koše určitě nepatří. ..." Ověřme tedy, zda má skutečně smysl Martingale metodu reálně obchodovat a pokud ano, pak za jakých omezujících podmínek.
Logika Metody Martingale
Metoda Martingale se asi nejsnáze popisuje na příkladu sázek v ruletě na barvu (červená nebo černá), kde budeme předpokládat, že počáteční sázka je €1, sázíme vždy na jednu ze dvou barev a výsledkem sázky je vždy prohra nebo výhra. Pokud prohrajeme, přicházíme o celou vsazenou částku, pokud vyhrajeme, získáváme tuto částku nazpět plus stejně velkou výherní částku. Abychom tedy pokryli celkovou ztrátu z předchozích po sobě jdoucích jednotlivých ztrátách a ještě získali nějaký profit, budeme po každé ztrátě velikost sázky zdvojnásobovat a po každé výhře se opět vrátíme na počáteční velikost sázky. Několik příkladů:
- Hned první výhra: zisk +€1
- Jedna ztráta a výhra: ztráta -€1, pak zisk +€2 = +€1
- Dvě ztráty a výhra: ztráta -€1, pak ztráta -€2, pak zisk +€4 = +€1
Jak je tedy vidět, každá taková sekvence N ztrát (N >= 0) a jedné výhry vede na výsledný zisk ekvivalentní velikosti počáteční vložené sázky.
Martingale metodu lze v případě tradingu použít opravdu mnoha různými způsoby. My zde budeme používat podobné nastavení jako ve zmíněném starším článku - budeme obchodovat EURUSD s nejmenší velikostí pozice 0,01 lotu a s konstantní vzdáleností StopLoss (SL) i TakeProfit (TP) 10 pipů od vstupní hodnoty.
Autor původního článku sice uvádí možnost nastavení různě vzdálených SL/TP podle střední velikosti výchylky ZigZag indikátoru na různých časových rámcích, my budeme nicméně předpokládat, že taková "optimalizace" vstupů nemá žádný efekt a tedy že je 50% pravděpodobnost (p) zasažení SL a 50% pravděpodobnost (q) zasažení TP, protože nejsme schopni odhadnout budoucí směr trhu a zasažení SL i TP je vzhledem k jejich stejné vzdálenosti od vstupu stejně pravděpodobné.
Stejnou pravděpodobnost výhry i prohry můžeme (při stejně vzdáleném SL i TP) předpokládat i tehdy, pokud je v trhu nějaký trend (krátkodobý nebo dlouhodobý), který ale trader neumí správně odhadnout a tedy otevírá efektivně náhodně Long nebo Short pozice.
Pravděpodobnost po sobě jdoucích ztrát
Z úvodu výše je zřejmé, že kritické pro vyhodnocení rizikovosti je zodpovězení otázky: "Jaká je pravděpodobnost, že během N obchodů narazíme na sekvenci K za sebou jdoucích ztrát?". Na rozdíl od kasina sice tato sekvence nemusí být pro účet zcela "likvidační", protože máme na účtu vždy jenom určitou povolenou páku (např. zmíněných 1:100) a tedy velikost požadovaného marginu nedovolí příliš velký propad na účtu na jednom obchodu (díky relativně blízkému SL). Pokud ale utrpíme ztrátu i na poslední velikosti pozice, kterou nám ještě margin požadavky povolují, snížíme hodnotu účtu tak, že se už nejspíše do černých čísel nedostaneme (alespoň ne Martingale metodou).
Zmíněnou pravděpodobnost lze spočítat pomocí následujícího vzorce (viz též krásné odvození zde):
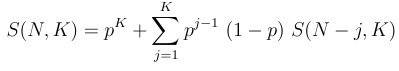
kde S(N, K) představuje hledanou hodnotu této pravděpodobnosti (hodnota mezi 0 a 1), K představuje onen "likvidační" počet ztrát v řadě a N počet obchodů, ve kterých přítomnost ztrát v řadě hledáme. Jak je vidět, vzorec je rekurzivní (tzn. odkazuje se na "znalost" hodnot S(N - j, K), tedy pravděpodobností nalezení K po sobě jdoucích ztrát v méně než N obchodech). Pro vyhodnocení samozřejmě použijeme počítačový program.
Zmíněná stránka (se vzorcem viz výše) uvádí rekurzivní kód v jazyce Python (volně dostupný pro všechny typy OS). V případě vyhodnocování pro velké množství obchodů (tzn. pro vysoké hodnoty N) narazíme na omezení hloubky rekurze (v Pythonu stejně jako v jiných jazycích), protože hloubka rekurze odpovídá právě N. Zde proto uvádíme upravenou verzi, která vede na stejné výsledky a neobsahuje rekurzi (zdrojový kód ke stažení zde):

Názvy proměnných pocetObchodu a pocetZtrat jsou dostatečně samopopisné (a používáme implicitní pravděpodobnost ztráty 50% viz předpoklady výše v textu).
Zkoušením různých hodnot si lze ověřit, že pravděpodobnost výskytu po sobě jdoucích ztrát je v daném počtu obchodů mnohdy větší, než by člověk čekal. Např. je nadpoloviční pravděpodobnost (cca 58%), že v sekvenci 252 obchodů (cca jeden obchod na pracovní den za rok) narazíme na sekvenci 5-ti po sobě jdoucích ztrát. Přitom 5 ztrát za sebou již vyžaduje otevření následující pozice 25 = 32 krát větší pozice než je naše základní pozice (v našem případě tedy 0,01 x 32 = 0,32 lotu).
Vyhodnocení rizika
Pravděpodobnosti dosažení N ztrát v sekvenci 252 obchodů (tedy přibližně jeden obchod každý obchodní den nezahrnující víkendy) jsou uvedeny v Tabulce 1 níže:

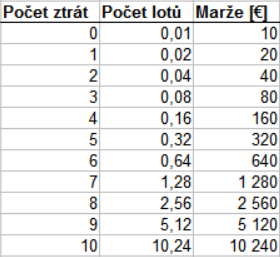
Pokud tedy budeme obchodovat tak, že "násobení velikosti sázky" budeme simulovat zdvojnásobením počtu lotů na každém obchodu následujícím po ztrátě, pak budeme otevírat obchody o velikosti 0,01 lotu, 0,02 lotu, 0,04 lotu, 0,08 lotu, atd. Očekávané parametry pozic dle velikosti (dané počtem za sebou jdoucích ztrát) jsou shrnuty v Tabulce 2.
Vyhodnocení očekávaného zisku
Je zřejmé, že při nekonečně velkém kapitálu a možnosti provést nekonečně mnoho obchodů je strategie vždy úspěšná. V realitě samozřejmě není splněna ani jedna z těchto podmínek. Podívejme se tedy na "očekávané" zisky v rozumných počtech obchodů s omezeným kapitálem.
Martingale obchodování můžeme rozdělit na sub-sekvence, kde je vždy nějaké množství za sebou jdoucích ztrát, které jsou následovány jednou výhrou (po ní následuje další sub-sekvence) nebo likvidací účtu tradera (resp. situací, kdy trader nebude schopen otevřít další větší pozici typicky díky požadavku na margin, na který účet už nebude stačit). V náslecujících odstavcích budeme počítat očekávanou hodnotou každé takové sub-sekvence.
Označme velikost "sázky" (představovanou trefením SL v základní velikosti pozice) jako L, pravděpodobnost ztráty jako q (pro odlišení od pravděpodobnosti výhry p = (1 - q)). Pravděpodobnost, že trader dosáhne právě m po sobě jdoucích ztrát je qm a celková ztráta v takovém případě bude:
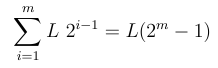
Pravděpodobnost, že trader neabsolvuje těchto m po sobě jdoucích ztrát je 1 - qm a v takovém případě získává trader profit L.
Očekávaný zisk na každou takovou sub-sekvenci proto lze spočítat jako (pravděpodobnost zisku krát velikost zisku minus pravděpodobnost ztráty krát velikost ztráty):
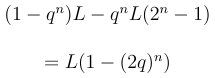
Z tohoto vyplývá, že trader může očekávat dlouhodobý zisk, pokud:
![]()
což nastává pouze v případě, kdy je pravděpodobnost ztráty q < 1/2 = 50%, ekvivalentně když pravděpodobnost zisku p > 50%.
Realita je ale taková, že bez schopnosti predikce pohybu trhu je pravděpodobnost ztráty vždy větší než pravděpodobnosti zisku. Stejně jako kasino si v případě sázek na černou a červenou barvu v americké ruletě zajišťuje výhodu na své straně oproti sázejícímu (pravděpodobnost prohry sázejícího je 10/19 > 50%), tak i v případě trhů je v nevýhodě trader díky spreadům (nákup za vyšší Ask a prodej za nižší Bid), komisím a dalším poplatkům, které budeme v dalším textu nazývat jako transakční poplatky. Očekávaný zisk je proto záporný, a to nezávisle na velikosti účtu, velikosti základní pozice nebo plánovaném počtu obchodů.
Typický zisk z malého množství obchodů
Jak bylo ale řečeno dříve, při "velkém" kapitálu a "malém" množství obchodů je celkem vysoká pravděpodobnost určité malé výhry a nízká pravděpodobnost velké ztráty.
Výpočet očekávané hodnoty je totiž pouze přesné vyjádření hodnoty průměru, jehož hodnota se bude blížit k očekávané hodnotě při zvyšování počtu pokusů (viz zákon velkých čísel).
Hodnota průměru ale může být zavádějící vzhledem k "běžné" zkušenosti jednotlivce. Např. publikování průměrného platu ve státě musí rozesmutnit určitě více než polovinu národa, protože plat většiny lidí bude pod tímto průměrem. To je dáno tím, že hodnota průměru je vyšší díky velmi vysokým platům velmi malé části národa. Místo průměru by bylo vhodnější uvádět hodnotu medianu (50%-ní percentil). Polovina měřených hodnot by měla být pod hodnotou medianu a polovina nad hodnotou medianu.
Pokud zde tedy mluvíme o "typickém zisku", máme na mysli právě median výsledných zisků ze sekvence N obchodů. Je zřejmé, že pokud jsou zisky spíše malé a ztráty spíše velké, bude výsledek ze sekvence pouze několika málo obchodů častěji kladný než záporný. Abychom si potvrdili toto tvrzení, provedeme simulaci viz níže.
Simulace náhodných sekvencí zisků a ztrát
Budeme předpokládat stejné nastavení algoritmu jako výše (EURUSD, 0,01 lotu, 10 pipů vzdálený SL i TP, 50%-ní pravděpodobnost zisku i ztráty a i nadále budeme ignorovat transakční náklady). Vzhledem k omezenému kapitálu budeme ale navíc počítat s tím, že pokud se rostoucí velikost pozice (vzhledem k po sobě jdoucím ztrátám) dostane k množství lotů, které by vyžadovalo margin, na který aktuální hodnota účtu nestačí, bude velikost následujícího obchodu opět na 0,01 lotu.
Simulace bude probíhat že proběhne vždy 1 000 iterací pro:
- tři různé velikosti účtů (10, 100 a 500 tisíc CZK)
- různě dlouhé sekvence obchodů (10 až 500 obchodů)
Příklad jedné iterace: Systém vygeneruje náhodně výhry a prohry ve 100 obchodech na účtu o velikosti 10 000 CZK a realizuje obchodování výše zmíněným způsobem. Průměrný zisk na jeden obchod z této iterace se pak spočítá jako:
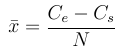
kde Cs je počáteční hodnota účtu a Ce je hodnota účtu po provedení zvolených N obchodů.
Na obrázku 1 níže je vyhodnocen (s vyhlazením) percentil (svislá osa) ztrátových hodnot zmíněného průměrného obchodu, a to pro všechny tři konkrétní velikosti účtu (různě barevné čáry). Např. vidíme, že s účtem o velikosti 10 000 korun (modrá čára) máme při 10-ti obchodech šanci dospět alespoň k nějakému zisku v cca 80% případů (100% minus zobrazených 20% výskytů ztrátového průměrného obchodu). Jak je ale dobře vidět z rychlého růstu křivky pro tuto velikost účtu, už při zvýšení počtu obchodů na 100 se dostáváme nepříjemně blízko 50%-nímu percentilu, tedy poloviční šanci na zisk nebo ztrátu. To je proto, že při tomto množství obchodů se často budeme dostávat do potřeby otevřít obchod, který bude vyžadovat marži, na kterou už zůstatek účtu nebude stačit. Naproti tomu při velikosti účtu 500 000 korun budeme jen zřídkakdy narážet na omezení marginem a hodnota percentilu se proto drží relativně nízko ještě i pro větší počet obchodů.

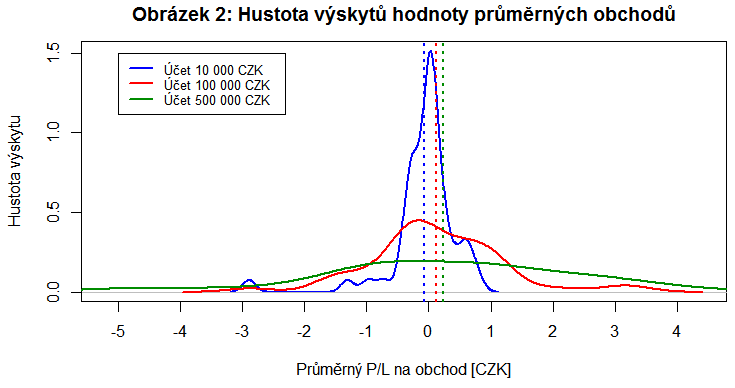
Na obrázku 2 níže je znázorněna vyhlazená hustota výskytů průměrného zisku z obchodu opět pro tři různé velikosti účtu (hodnoty pro různé počty obchodů jsou smíchány dohromady). Je zřejmé, že celkový průměrný zisk na obchod pro danou velikost účtu (vyznačen tečkovanými vertikálami odpovídající barvy) se ve všech třech případech pohybuje velmi blízko nuly (< 1 koruna) a při započítání transakčních poplatků je tedy ve všech případech průměrný obchod jednoznačně ztrátový.
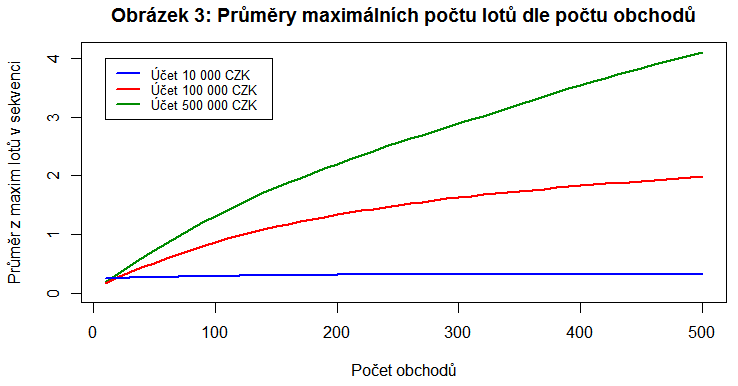
Na obrázku 3 níže jsou znázorněny (opět vyhlazené) průměry z maximálních velikostí pozic (v počtech lotů) dosažených ve všech sekvencích obchodů na účtu dané velikosti. Hodnoty pro 10-ti tisícový účet zůstávají blízko počáteční velikosti pozice, protože na tak malém účtu ani větší pozice otevřít nemůžeme. Zajímavá je situace například u 500-ti tisícového účtu, kde je vidět, že v případě 500 obchodů se dostáváme (v průměru) na maximální velikosti pozice kolem 4 lotů (tedy 400x počáteční velikost pozice). Medián maximálních pozic by byl nejspíše výrazně níže, protože se v několika málo případech stane, že budeme muset otevírat opravdu velkou pozici a průměry se nám tím hodně navýší.
Závěr
Z teoretického hlediska tedy nemá metoda Martingale smysl určitě. Při započtení transakčních poplatků nemá Martingale smysl pro dlouhodobé obchodování ani prakticky.
Metoda má určité opodstatnění ve zmíněném jednom okrajovém případě, kdy s velkým kapitálem chceme s velkou pravděpodobností udělat malý zisk během malého počtu obchodů.




